数学公式(Latex)

发表于 更新于 Disqus：

数学公式(LATEX)

测试：

行内公式测试：\(A_a\)，希腊字母：\(\beta\)

行间公式测试： \[ f(t)=a_t \] 换行测试

  1. 行内 \(\begin{gather*}a_2\\d^5\end{gather*}\) 行内测试完毕

  2. 行间 \[ \begin{gather*} a_2\\ d^5 \end{gather*}、 \]

可以正常渲染公式。

常用

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
\begin{gather*}
上下标：y_下标=x^上标\\
分式与求导:\frac{分子}{分母}\\
求导：求导其实就是输入字母\\
积分：\int_{积分下限}^{积分上限}{积分变量}d被积变量\\
大括号:
\begin{cases}
括号内第一行\\
括号内第二行\\
\end{cases}\\
极限:\lim_{n\rightarrow\infty}{x}\\
\vec{向量}\\
\sum_{n=起始值}^{终值}{a_n}\\
\prod_{n=起始值}^{终值}{a_n}\\
\sqrt e\\
\approx
\end{gather*}

\[ \begin{gather*} 上下标：y_下标=x^上标\\ 分式与求导:\frac{分子}{分母}\\ 求导：求导其实就是输入字母\\ 积分：\int_{积分下限}^{积分上限}{积分变量}d被积变量\\ 大括号: \begin{cases} 括号内第一行\\ 括号内第二行\\ \end{cases}\\ 极限:\lim_{n\rightarrow\infty}{x}\\ \vec{向量}\\ \sum_{n=起始值}^{终值}{a_n}\\ \prod_{n=起始值}^{终值}{a_n}\\ \sqrt e\\ \approx \end{gather*} \]

运算符

1
2
3
4
5
6
7
8
+
-
\times
/
\div
\cdot
\#
\%

\[ + - \times / \div \cdot \# \% \]

1
2
3
4
5
6
\cap
\cup
\land
\lor
\sqcup
\sqcap

\[ \cap \cup \land \lor \sqcup \sqcap \]

1
2
3
4
5
6
\circ
\ast
\star
\otimes
\oplus
\odot

\[ \circ \ast \star \otimes \oplus \odot \]

1
2
3
4
\pm
\mp
\dotplus
\divideontimes

\[ \pm \mp \dotplus \divideontimes \]

约等于

1
2
3
4
5
6
7
=
= \not
\equiv
\approx
\approxeq
\cong
\sim

\[ = = \not \equiv \approx \approxeq \cong \sim \]

比较

1
2
3
4
5
6
<
>\\
0 \le \omega t \le \pi \\
\ge
\gg
\ll

\[ < >\\ 0 \le \omega t \le \pi \\ \ge \gg \ll \]

1
2
3
4
5
6
\curlyeqprec
\curlyeqsucc
\prec
\succ
\preceq
\succeq

\[ \curlyeqprec \curlyeqsucc \prec \succ \preceq \succeq \]

集合/逻辑相关

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
\in
\owns \not
\subset \not
\supset
\subseteq
\supseteq
\\
\cap
\cup
\land
\lor
\\
\neg
\emptyset
\varnothing
\\
\because
\forall
\exists
\therefore

\[ \in \owns \not \subset \not \supset \subseteq \supseteq \\ \cap \cup \land \lor \\ \neg \emptyset \varnothing \\ \because \forall \exists \therefore \]

箭头

1
2
3
4
5
6
7
8
9
\gets
\leftarrow
\to
\rightarrow
\leftrightarrow
\\
\uparrow
\downarrow
\updownarrow

\[ \gets \leftarrow \to \rightarrow \leftrightarrow \\ \uparrow \downarrow \updownarrow \]

1
2
3
4
5
6
7
8
\Leftarrow
\Rightarrow
\Leftrightarrow
\iff
\\
\Uparrow
\Downarrow
\Updownarrow

\[ \Leftarrow \Rightarrow \Leftrightarrow \iff \\ \Uparrow \Downarrow \Updownarrow \]

1
2
3
4
\nearrow
\searrow
\swarrow
\nwarrow

\[ \nearrow \searrow \swarrow \nwarrow \]

1
2
3
4
5
\leftharpoonup
\leftharpoondown
\rightharpoonup
\rightharpoondown
\rightleftharpoons

\[ \leftharpoonup \leftharpoondown \rightharpoonup \rightharpoondown \rightleftharpoons \]

1
2
3
4
\mapsto
\leadsto
\hookleftarrow
\hookrightarrow

\[ \mapsto \leadsto \hookleftarrow \hookrightarrow \]

1
2
3
4
5
6
7
\longleftarrow
\longrightarrow
\longleftrightarrow
\Longleftarrow
\Longrightarrow
\Longleftrightarrow
\longmapsto

\[ \longleftarrow \longrightarrow \longleftrightarrow \Longleftarrow \Longrightarrow \Longleftrightarrow \longmapsto \]

1
2
3
4
5
6
\xrightarrow{over}
\xrightarrow[over]{}
\xrightarrow[under]{over}
\xleftarrow[]{over}
\xleftarrow[under]{}
\xleftarrow[under]{over}

\[ \xrightarrow{over} \xrightarrow[over]{} \xrightarrow[under]{over} \xleftarrow[]{over} \xleftarrow[under]{} \xleftarrow[under]{over} \]

空格间距

1
2
3
4
\begin{gather*}
\sf{紧贴 + 无空格 + 小空格 + 中空格 + 大空格 + 真空格 + 双真空格}\\
\it{a\!b + ab + a\,b + a\;b + a\ b + a\quad b + a\qquad b}\\
\end{gather*}

\[ \begin{gather*} \sf{紧贴 + 无空格 + 小空格 + 中空格 + 大空格 + 真空格 + 双真空格}\\ \it{a\!b + ab + a\,b + a\;b + a\ b + a\quad b + a\qquad b}\\ \end{gather*} \]

希腊字母表

希腊字母 希腊字母 希腊字母 希腊字母
\(\alpha\) \(\beta\) \(\gamma\) \(\phi\)
\(\nu\) \(\epsilon\) \(\varepsilon\) \(\varrho\)
\(\Delta\) \(\pi\) \(\psi\) \(\varDelta\)
\(\varPsi\) \(\zeta\) \(\kappa\) \(\xi\)
\(\chi\) \(\varkappa\) \(\varsigma\) \(\Theta\)
\(\Omega\) \(\varTheta\) \(\varSigma\) \(\varOmega\)
\(\lambda\) \(\omicron\) \(\tau\) \(\psi\)
\(\varphi\) \(\Lambda\) \(\Upsilon\) \(\varLambda\)
\(\delta\) \(\theta\) \(\mu\) \(\pi\)
\(\omega\) \(\varpi\) \(\digamma\) \(\partial\)
\(\imath\) \(\jmath\) \(\aleph\) \(\hbar\)
No. Lowercase Uppercase English IPA
\(1\) \(\alpha\) \(A\) \(alpha\) /'ælfə/
\(2\) \(\beta\) \(B\) \(beta\) /'bi:tə/or/'beɪtə/
\(3\) \(\gamma\) \(\Gamma\) \(gamma\) /'gæmə/
\(4\) \(\delta\) \(\Delta\) \(delta\) /'deltə/
\(5\) \(\epsilon\) \(E\) \(epsilon\) /'epsɪlɒn/
\(6\) \(\zeta\) \(Z\) \(zeta\) /'zi:tə/
\(7\) \(\eta\) \(H\) \(eta\) /'i:tə/
\(8\) \(\theta\) \(\Theta\) \(theta\) /'θi:tə/
\(9\) \(\iota\) \(I\) \(iota\) /aɪ'əʊtə/
\(10\) \(\kappa\) \(K\) \(kappa\) /'kæpə/
\(11\) \(\lambda\) \(\lambda\) \(lambda\) /'læmdə/
\(12\) \(\mu\) \(M\) \(mu\) /mju:/
\(13\) \(\nu\) \(N\) \(nu\) /nju:/
\(14\) \(\xi\) \(\Xi\) \(xi\) /ksi/or/'zaɪ/or/'ksaɪ/
\(15\) \(\omicron\) \(O\) \(omicron\) /əu'maikrən/or/'ɑmɪ,krɑn/
\(16\) \(\pi\) \(\Pi\) \(pi\) /paɪ/
\(17\) \(\rho\) \(P\) \(rho\) /rəʊ/
\(18\) \(\sigma\) \(\Sigma\) \(sigma\) /'sɪɡmə/
\(19\) \(\tau\) \(T\) \(tau\) /tɔ:/or/taʊ/
\(20\) \(\upsilon\) \(\Upsilon\) \(upsilon\) /'ipsilon/or/'ʌpsilɒn/
\(21\) \(\phi\) \(\Phi\) \(phi\) /faɪ/
\(22\) \(\chi\) \(X\) \(chi\) /kaɪ/
\(23\) \(\psi\) \(\Psi\) \(psi\) /psaɪ/
\(24\) \(\omega\) \(\Omega\) \(omega\) /'əʊmɪɡə/or/oʊ'meɡə/

矩阵

1
2
3
4
A = \begin{matrix}
a & b\\
c & d
\end{matrix}

\[ A = \begin{matrix} a & b\\ c & d \end{matrix} \]

1
2
3
4
B = \begin{pmatrix}
a & b\\
c & d
\end{pmatrix}

\[ B = \begin{pmatrix} a & b\\ c & d \end{pmatrix} \]

1
2
3
4
C = \begin{vmatrix}
a & b\\
c & d
\end{vmatrix}

\[ C = \begin{vmatrix} a & b\\ c & d \end{vmatrix} \]

1
2
3
4
D = \begin{bmatrix}
a & b\\
c & d
\end{bmatrix}

\[ D = \begin{bmatrix} a & b\\ c & d \end{bmatrix} \]

1
2
3
4
E = \begin{Vmatrix}
a & b\\
c & d
\end{Vmatrix}

\[ E = \begin{Vmatrix} a & b\\ c & d \end{Vmatrix} \]

1
2
3
4
F = \begin{Bmatrix}
a & b\\
c & d
\end{Bmatrix}

\[ F = \begin{Bmatrix} a & b\\ c & d \end{Bmatrix} \]

1
2
3
4
5
6
7
8
[A\ b] = 
\begin{bmatrix}
\begin{array}{c c c|c}
a_{11} & a_{12} & a_{13} & b_1\\
a_{21} & a_{22} & a_{23} & b_2\\
a_{31} & a_{32} & a_{33} & b_3\\
\end{array}
\end{bmatrix}

\[ [A\ b] = \begin{bmatrix} \begin{array}{c c c|c} a_{11} & a_{12} & a_{13} & b_1\\ a_{21} & a_{22} & a_{23} & b_2\\ a_{31} & a_{32} & a_{33} & b_3\\ \end{array} \end{bmatrix} \]

1
2
3
4
5
6
7
\begin{array}{c:c:c}
a & b & c \\ 
\hline
d & e & f \\
\hdashline
 g & h & i
\end{array}

\[ \begin{array}{c:c:c} a & b & c \\ \hline d & e & f \\ \hdashline g & h & i \end{array} \]

1
2
3
4
5
6
L_{n\times n} = \begin{bmatrix}
a_{11} & a_{12} & \cdots & a_{1n} \\ 
a_{21} & a_{22} & \cdots & a_{2n} \\ 
\vdots & \vdots &\ddots & \vdots\\
a_{n1} & a_{n2} & \cdots & a_{nn} \\ 
\end{bmatrix}

\[ L_{n\times n} = \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots &\ddots & \vdots\\ a_{n1} & a_{n2} & \cdots & a_{nn} \\ \end{bmatrix} \]

1
2
3
4
5
6
Y = \begin{bmatrix}
x^{(0)}(2) \\ 
x^{(0)}(3)  \\ 
\vdots \\
x^{(0)}(18)  \\ 
\end{bmatrix}

\[ B = \begin{bmatrix} -\frac{1}{2}(x^{(1)}(1)+x^{(1)}(2)) & 1 \\ -\frac{1}{2}(x^{(1)}(2)+x^{(1)}(3)) & 1 \\ \vdots & \vdots \\ -\frac{1}{2}(x^{(1)}(17)+x^{(1)}(18)) & 1 \\ \end{bmatrix} \]

1
2
3
4
5
6
Y = \begin{bmatrix}
x^{(0)}(2) \\ 
x^{(0)}(3)  \\ 
\vdots \\
x^{(0)}(18)  \\ 
\end{bmatrix}

\[ Y = \begin{bmatrix} x^{(0)}(2) \\ x^{(0)}(3) \\ \vdots \\ x^{(0)}(18) \\ \end{bmatrix} \]

1
2
3
4
5
6
7
8
9
10
\hat{\textbf{u}} = 
\begin{bmatrix}
\hat{a} \\ 
\hat{b} \\ 
\end{bmatrix}
=\textbf{(B}^{T}\textbf{B}\textbf{)}^{-1}\textbf{B}^{T}\textbf{Y}
=\begin{bmatrix}
\hat{a} \\ 
\hat{b} \\ 
\end{bmatrix}

\[ \hat{\textbf{u}} = \begin{bmatrix} \hat{a} \\ \hat{b} \\ \end{bmatrix} =\textbf{(B}^{T}\textbf{B}\textbf{)}^{-1}\textbf{B}^{T}\textbf{Y} =\begin{bmatrix} \hat{a} \\ \hat{b} \\ \end{bmatrix} \]

1
2
\hat{a}=\\
\hat{b}= \\

\[ \hat{a}=\\ \hat{b}= \\ \]

1
\frac{dx^{(1)}}{dt}+\hat{a}x^{(1)}=\hat{b}

\[ \frac{dx^{(1)}}{dt}+\hat{a}x^{(1)}=\hat{b} \]

列式/方程组

1
2
3
4
\begin{aligned}
f(x) &= (x+1)^2\\
&= x^2 + 2x + 1
\end{aligned}

\[ \begin{aligned} f(x) &= (x+1)^2\\ &= x^2 + 2x + 1 \end{aligned} \]

1
2
3
4
f(x) = \begin{cases}
a &\text{if b}\\
b &\text{if a}\\
\end{cases}

\[ f(x) = \begin{cases} a &\text{if b}\\ b &\text{if a}\\ \end{cases} \]

1
2
3
4
5
6
\begin{cases}
\begin{aligned}
x + 2y &= 1\\
3x - y &= 5
\end{aligned}
\end{cases}

\[ \begin{cases} \begin{aligned} x + 2y &= 1\\ 3x - y &= 5 \end{aligned} \end{cases} \]

注释图片

1
2
3
4
5
6
7
8
9
10
<center>
    <img style="border-radius: 0.3125em;
    box-shadow: 0 2px 4px 0 rgba(34,36,38,.12),0 2px 10px 0 rgba(34,36,38,.08);" 
    src="图片地址" alt="image-20210531181704173" />
    <br>
    <div style="color:orange; border-bottom: 1px solid #d9d9d9;
    display: inline-block;
    color: #999;
    padding: 2px;">注释</div>
</center>
image-20210531181704173
注释

字体

字体名 样式

修饰符

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
\hat{\theta}
\widehat{AB}
\\
\bar{y}
\overline{AB}
\\
\tilde{a}
\widetilde{ac}
\\
\bar{a}
\acute{a}
\check{a}
\grave{a}
\\
\dot{a}
\ddot{a}

\[ \hat{\theta} \widehat{AB} \\ \bar{y} \overline{AB} \\ \tilde{a} \widetilde{ac} \\ \bar{a} \acute{a} \check{a} \grave{a} \\ \dot{a} \ddot{a} \]

括号

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
\begin{gather*}
(
\big(
\Big(
\bigg(
\Bigg(
\\
[]
<>
|绝对值|
\{\}
\\
\lgroup x \rgroup
\lVert a \rVert
\lceil 2.6 \rceil
\lfloor 1.2 \rfloor
\\
\ulcorner
\urcorner
\llcorner
\lrcorner
\end{gather*}

\[ \begin{gather*} ( \big( \Big( \bigg( \Bigg( \\ [] <> |绝对值| \{\} \\ \lgroup x \rgroup \lVert a \rVert \lceil 2.6 \rceil \lfloor 1.2 \rfloor \\ \ulcorner \urcorner \llcorner \lrcorner \end{gather*} \]

偏微分

1
\frac{\partial u}{\partial t}= h^2 \left( \frac{\partial^2 u}{\partial x^2} +\frac{\partial^2 u}{\partial y^2}+ \frac{\partial^2 u}{\partial z^2}\right)

\[ \frac{\partial u}{\partial t}= h^2 \left( \frac{\partial^2 u}{\partial x^2} +\frac{\partial^2 u}{\partial y^2}+ \frac{\partial^2 u}{\partial z^2}\right) \]

图形

1
2
3
4
5
6
7
8
9
10
11
12
13
14
\Box
\square
\blacksquare
\triangle
\triangledown
\blacktriangle
\diamond
\Diamond
\star
\bigstar
\circ
\bullet
\bigcirc
\bigodot

\[ \Box \square \blacksquare \triangle \triangledown \blacktriangle \diamond \Diamond \star \bigstar \circ \bullet \bigcirc \bigodot \]

1
2
3
4
\diamondsuit
\clubsuit
\heartsuit
\spadesuit

\[ \diamondsuit \clubsuit \heartsuit \spadesuit \]

1
2
3
4
5
\angle
\measuredangle
\top
\bot
\infty

\[ \angle \measuredangle \top \bot \infty \]

1
2
3
4
5
\checkmark
\dagger
\ddagger
\yen
\$

\[ \checkmark \dagger \ddagger \yen \$ \]

变换符号

1
2
3
4
%拉氏变换：
\mathscr{L}{f(t)}
\mathcal{L}
%傅里叶变换：

\[ \mathscr{L}\{f(t)\}\quad \mathcal{L} \]

typroa框图（博客不支持）

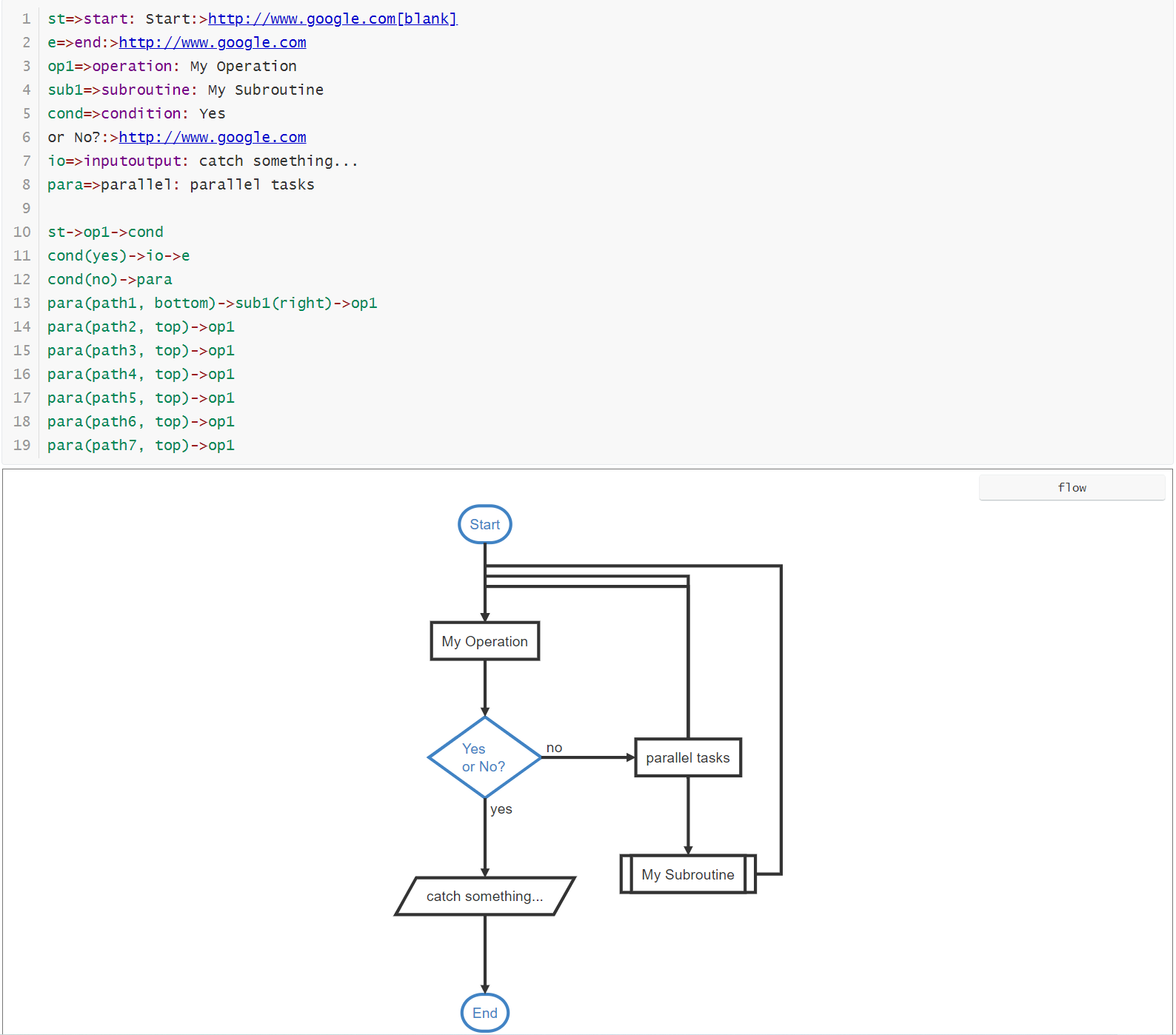
流程图

语法说明：

  • graph LR： 这一行说明要绘制的图形的方向。
    • LR：从左到右，left to right
    • RL：从右到左，right to left
    • TB：从上到下，top to bottom
    • BT：从下到上，bottom to top
  • 定义节点：有两种定义节点的方式
    • 可以直接输入文字信息作为节点名称: node1
    • 也可以在节点名称前加一个id的形式：id2(node2)，这样后续可以通过id1来引用node1这个节点。
  • 节点图形形状：
    • 默认：方形
    • (node2）: 圆角
    • {[node3]) ：椭圆
  • 条件节点：在绘制流程图中会经常用到条件节点，在Mermaid中也可以实现的。
1
2
3
4
5
6
7
8
9
st=>start: 开始框
op=>operation: 处理框
cond=>condition: 判断框(是或否?)
sub1=>subroutine: 子流程
io=>inputoutput: 输入输出框
e=>end: 结束框
st->op->cond
cond(yes)->io->e
cond(no)->sub1(right)->op
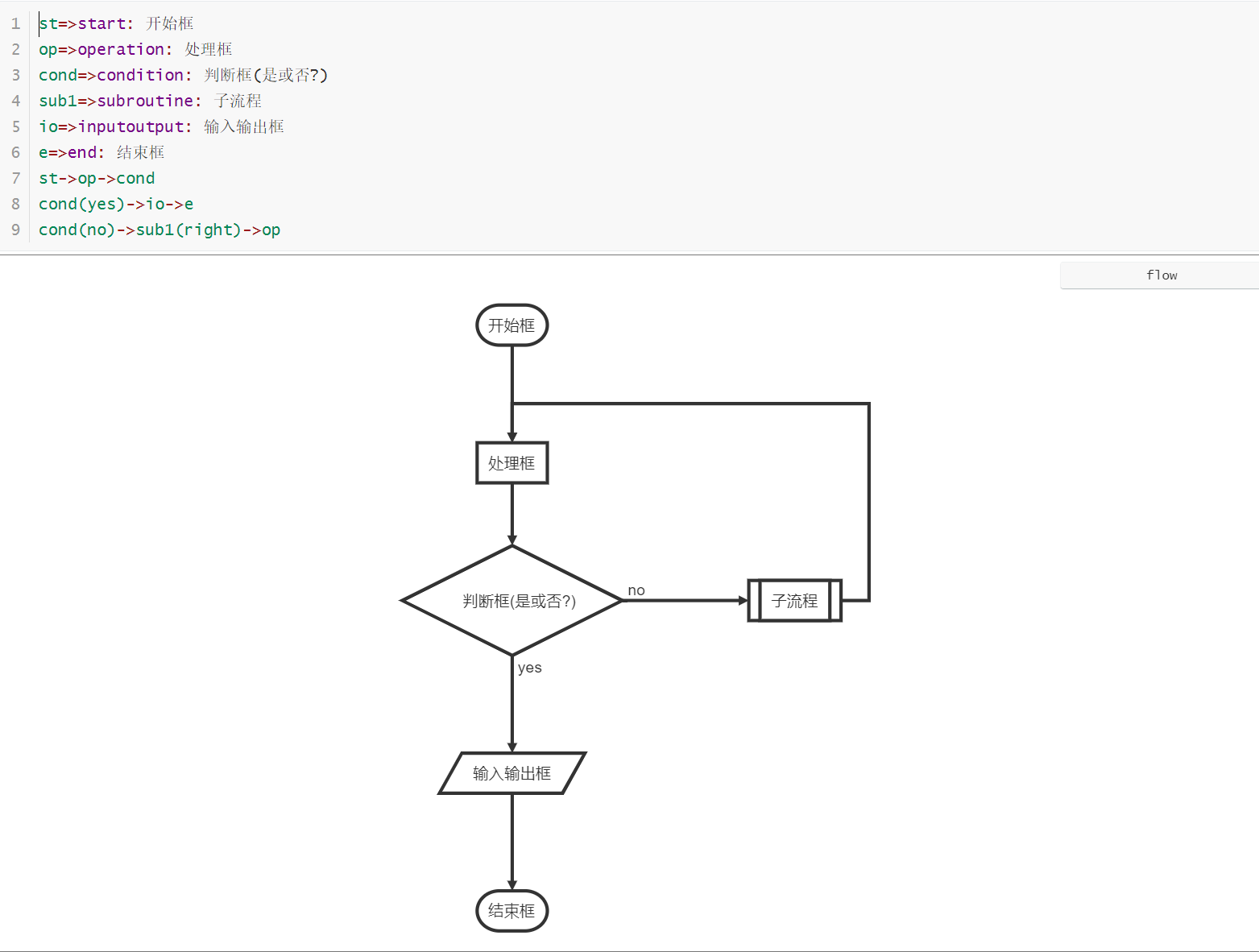
image-20220225234024945 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
st=>start: Start:>http://www.google.com[blank]
e=>end:>http://www.google.com
op1=>operation: My Operation
sub1=>subroutine: My Subroutine
cond=>condition: Yes
or No?:>http://www.google.com
io=>inputoutput: catch something...
para=>parallel: parallel tasks

st->op1->cond
cond(yes)->io->e
cond(no)->para
para(path1, bottom)->sub1(right)->op1
para(path2, top)->op1
para(path3, top)->op1
para(path4, top)->op1
para(path5, top)->op1
para(path6, top)->op1
para(path7, top)->op1
image-20220225234115328