大学物理实验绘图

发表于 更新于 Disqus：

[TOC]

标准程序

数据标识标准

实验测量数据统一使用measure的首字母m做下标表示

标准数据使用standard的首字母s做下标表示

通过拟合方程计算得出的结果使用calculate的首字母c做下标表示

相对误差计算程序

1
2
3
4
5
6
7
8
9
10
%计算相对误差
prompt = '请输入测量值Xm=';
Xm = input(prompt);
prompt = '请输入标准值Xs=';
Xs = input(prompt);
%计算相对误差
RelEor =abs((Xm-Xs)/Xs)*100;
R=round(RelEor,2);
disp('计算得相对误差为:')
disp([num2str(R),'%']);

描点作图

1
2
3
Xm=[];
Ym=[];
plot(Xm,Ym);

求平均值

1
2
3
Xm=[];
Ym=[];y
Xm_mean=mean(Xm,Ym);

一元线性回归

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
%一元线性回归分析

%写入数据:
Xm=[-1.875,-1.474,-1.262,-0.709,-0.586];
Ym=[8.214,7.408,6.879,5.490,5.196];

%进行回归分析
[p,s]=polyfit(Xm,Ym,1);%p中存储有k和b的信息，s中存的信息我不知道
Yc=p(1)*Xm+p(2);
R2=1 - (sum((Yc- Ym).^2) / sum((Ym - mean(Ym)).^2));

%打印回归结果
disp('打印回归分析结果:');
fprintf('y=%fx+%f\n',p(1),p(2));
fprintf('R^2=%f\n',R2);

%绘图
plot(Xm,Ym,'o');%数据点图
Xp=[min(Xm):0.1:max(Xm)];
Yp=p(1)*Xp+p(2);
hold on;
plot(Xp,Yp);%拟合曲线图
grid on;

绘图

1
2
3
title("标题",'FontName','SimHei');
xlabel("X轴",'FontName','SimHei');
ylabel("Y轴",'FontName','SimHei');

隐函数族图像绘制

1
2
3
4
5
6
7
8
9
10
11
function z = z(x,y,k)
z = 0.5*x^2+3*x*y+0.5*y^2-k;
end

%k限定着函数族的范围
k = -10;
while k < 10
    k = k + 1;
    ezplot(@(x,y)z(x,y,k));
    hold on;
end

实验数据处理

非线性负组电路元件伏安特性

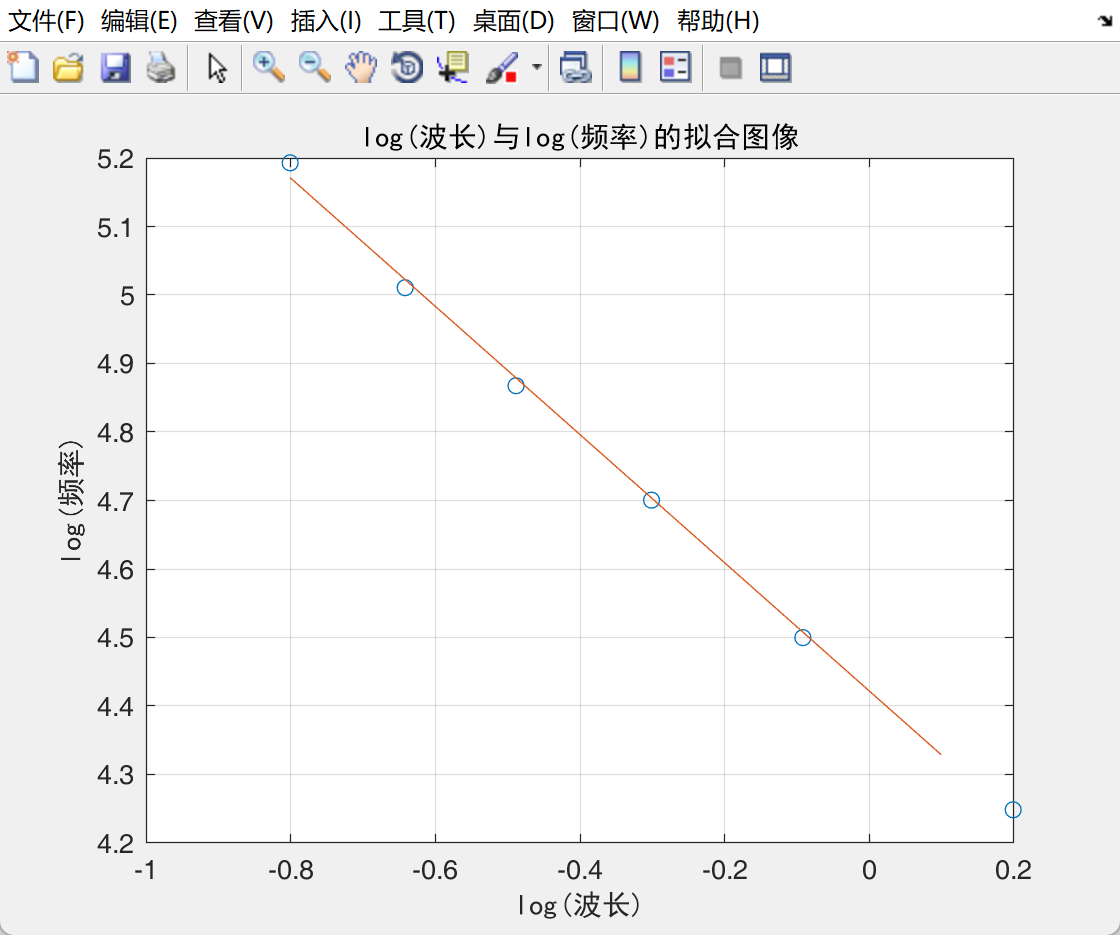
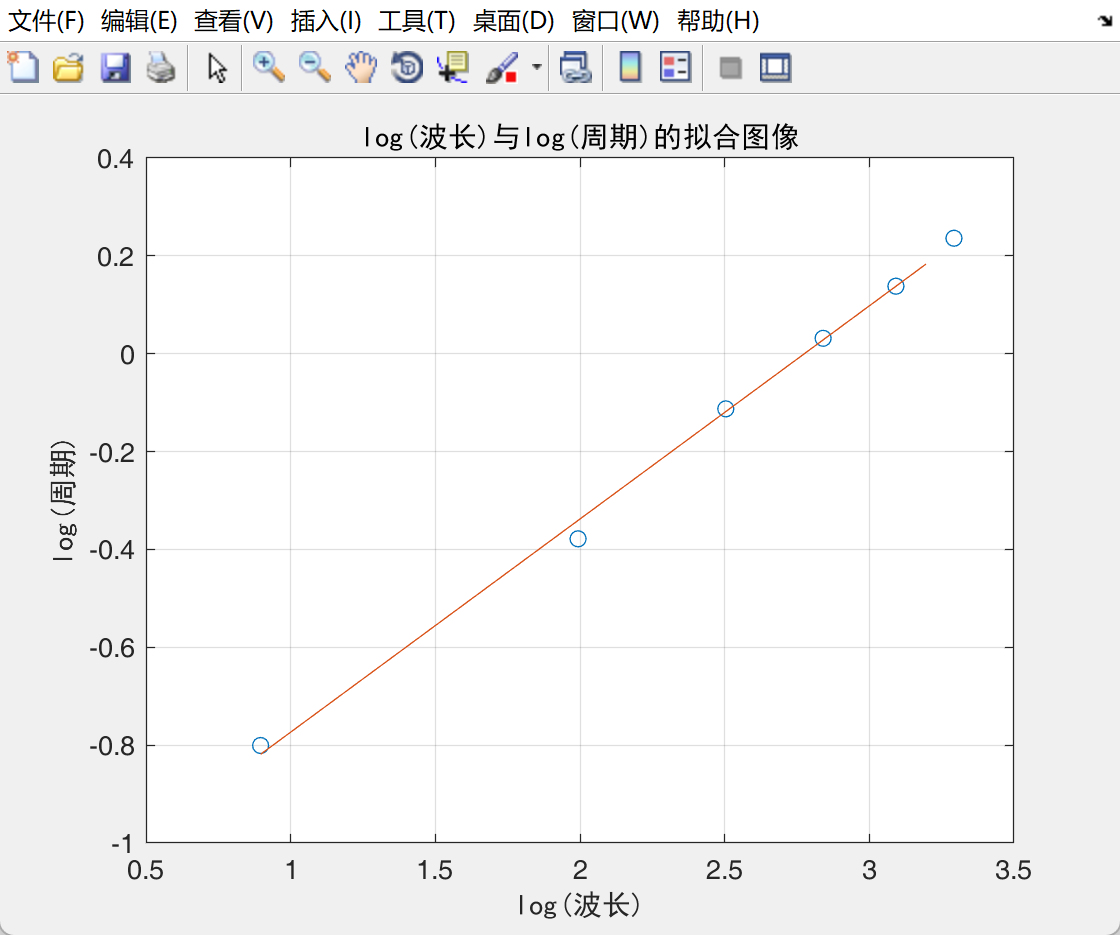
1
2
3
4
5
6
7
8
9
10
clear
clc
Ym=[-0.002,-0.011,-0.031,-0.046,-0.072,-0.140,-0.618,-0.731,-0.894,-1.148,-1.582,-1.672,-1.688,-1.748,-1.901,-2.068,-2.250,-2.677,-2.926,-3.206,-3.888,-4.311,-4.806,-6.106,-6.276,-6.493,-6.618,-6.803,-7.195,-8.105,-8.656,-9.267,-9.962,-10.353,-10.766,-11.214,-11.214,-11.533,-11.645,-11.893,-12.094,-12.146,-12.273,-12.352,-12.457];
R=[300,600,900,1000,1100,1200,1300,1305,1310,1315,1320,1325,1330,1350,1400,1450,1500,1600,1650,1700,1800,1850,1900,2000,2010,2020,2030,2040,2060,2100,2120,2140,2160,2170,2180,2190,2200,2700,3000,4000,5000,6000,8000,10000,15000];
I=Ym./R;
Xm=I;
plot(Xm,Ym);%数据点图
title("非线性负组电路元件伏安特性",'FontName','SimHei');
xlabel("电流(A)",'FontName','SimHei');
ylabel("电压(V)",'FontName','SimHei');

弦线上波的传播规律

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
%固定张力和线密度
f=[70 90 110 130 150 180];
lamt=[1.22 0.9122 0.74 0.6136 0.5264 0.449];


%一元线性回归分析

%写入数据:
Xm=log(lamt);
Ym=log(f);

%进行回归分析
[p,s]=polyfit(Xm,Ym,1);%p中存储有k和b的信息，s中存的信息我不知道
Yc=p(1)*Xm+p(2);
R2=1 - (sum((Yc- Ym).^2) / sum((Ym - mean(Ym)).^2));

%打印回归结果
disp('打印回归分析结果:');
fprintf('y=%fx+%f\n',p(1),p(2));
fprintf('R^2=%f\n',R2);

%绘图
plot(Xm,Ym,'o');%数据点图
Xp=[min(Xm):0.1:max(Xm)];
Yp=p(1)*Xp+p(2);
hold on;
plot(Xp,Yp);%拟合曲线图
grid on;
title("log(波长)与log(频率)的拟合图像",'FontName','SimHei');
xlabel("log(波长)",'FontName','SimHei');
ylabel("log(频率)",'FontName','SimHei');

Xm
Ym

image-20211106173254618

1
2
3
4
5
6
7
8
9
10
11
12
打印回归分析结果:
y=-0.935900x+4.421856
R^2=0.998356

Xm =

    0.1989   -0.0919   -0.3011   -0.4884   -0.6417   -0.8007


Ym =

    4.2485    4.4998    4.7005    4.8675    5.0106    5.1930
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
%固定频率和线密度
T=[2.45 7.34 12.23 17.12 22.02 26.91];
lamt=[0.449 0.6850 0.8934 1.032 1.148 1.2662];


%一元线性回归分析

%写入数据:
Xm=log(T);
Ym=log(lamt);

%进行回归分析
[p,s]=polyfit(Xm,Ym,1);%p中存储有k和b的信息，s中存的信息我不知道
Yc=p(1)*Xm+p(2);
R2=1 - (sum((Yc- Ym).^2) / sum((Ym - mean(Ym)).^2));

%打印回归结果
disp('打印回归分析结果:');
fprintf('y=%fx+%f\n',p(1),p(2));
fprintf('R^2=%f\n',R2);

%绘图
plot(Xm,Ym,'o');%数据点图
Xp=[min(Xm):0.1:max(Xm)];
Yp=p(1)*Xp+p(2);
hold on;
plot(Xp,Yp);%拟合曲线图
grid on;
title("log(波长)与log(周期)的拟合图像",'FontName','SimHei');
xlabel("log(波长)",'FontName','SimHei');
ylabel("log(周期)",'FontName','SimHei');

Xm
Ym

image-20211106173033589

1
2
3
4
5
6
7
8
9
10
11
12
13
打印回归分析结果:
y=0.435631x+-1.209052
R^2=0.997443

Xm =

    0.8961    1.9933    2.5039    2.8402    3.0920    3.2925


Ym =

   -0.8007   -0.3783   -0.1127    0.0315    0.1380    0.2360

磁滞曲线

1
2
3
4
5
6
7
8
9
10
11
12
13
x=0:0.2:3;
>> y1=[-1.4,-1.2,-1.1,-1.0,-0.9,-0.8,-0.6,-0.3,0,0.4,0.7,1.1,1.4,1.8,1.9,2.0];
>> y2=[1.4 1.3 1.4 1.4 1.6 1.6 1.6 1.7 1.7 1.8 1.8 1.8 1.8 1.9 2.0 2.0];

plot(x,y1)
>> hold on
>> plot(x,y2)
>> plot(-x,-y2)
>> hold on
>> plot(-x,-y1)

title("磁滞曲线",'FontName','SimHei');

untitled