电子学

发表于 2022-02-27 更新于 2022-09-08 Disqus：

电子学

前言

本书主要参考尼曼（Donald A. Neamen）的《电子电路分析与设计（第四版）》（Microelectronics: Circuit Analysis And Design Forth Edition）写成。

半导体器件及其基本应用

半导体

在电路课和物理课上我们已经学习了一些电子器件，例如最典型的器件——电阻器。电阻器是导体，其最重要的性质“电阻”表示了导体对于电流的阻碍性质。除此之外我们还学习了电容和电感；电感的性质存在于线圈之中，线圈是使用导体制成的；电容则是导体极板中间夹着一个绝缘体介质形成。如此归纳，我们会发现在之前的课程之中，我们了解的范畴始终存在于导体和绝缘体之中，而半导体材料制作而成的器件却从未被提及。所以，在“半导体”这一节中，我们将注意力集中在半导体上，从研究半导体自身的性质开始，最终我们将得到一个简单的半导体器件。

正式开始本节前，我们简单地回顾一下中学的知识，以下这些是作者默认读者已经了解了的知识。

导体中存在大量可以自由移动的电子，称之为自由电子（free electron）。自由电子在受到外电场或外磁场的作用时，能够在物质中自由移动。
导体中自由电子的定向移动形成了电流，电流（current）的定义式为 $i=\frac{dq}{dt}$。
载流子（charge carrier）指可以自由移动的带有电荷的物质微粒，是物质中电流形成的原因，导体中的载流子是电子。
在半导体中存在两种载流子——电子（electron）和空穴（hole）。空穴是电子移动后留下的空位，从物理模型上可以将空穴看作是正电子。在半导体中，电子和空穴两种载流子共同形成半导体中的电流。

本征半导体（intrinsic semiconductor）

本征半导体是指纯净（pure）的半导体

本征半导体的概念是我们应当格外注意的，因为这不是一个偏日常化和口语化的词语，但是在这里它的含义却是十分简单——本征，不过就是纯净不含杂质的意思。

强调材料的纯度似乎是一件奇怪的事情，因为常识中我们通常认为提纯是必须的，无需额外强调的。例如我们不会强调一个钢筋的纯度，但是我们知道

本征半导体是指纯净的半导体，强调这个词似乎暗示着有一种不纯净的半导体的存在，并且这种不纯净的半导体的存在是十分有必要的。

二极管及其基本电路

TODO

三极管及其基本电路

TODO

场效应管及其基本电路

TODO

模拟电子技术

TODO

数字电子技术

TODO

运算放大器电路

分析顺序

图像
公式
结论

反相放大电路
- 反相放大电路连接方式如图所示：
- 反相放大电路增益 $A_v$：
  
  假设运算放大器是理想的，即
  - 开环增益 $A_{od}=\infty$：故输入信号 $v_1$ 和 $v_2$ 是相等的。且由于 $v_2$ 与地面连接，故 $v_2$ 是“接地”，而 $v_1$ 是“虚地”。
  - 输入阻抗大小为 $\infty$：流入运算放大器的电流为 $0$ 。
  理想运放约束+基尔霍夫定律可得： \[ \begin{cases} \begin{aligned} &\frac{v_{i_1}-v_1}{R_1}=\frac{v_1-v_o}{R_2}\\\\ &v_1=0 \end{aligned} \end{cases} \quad \Longrightarrow \quad A_v=\frac{v_o}{v_{i_1}}=-\frac{R_2}{R_1}\tag{1-1} \]
- 结论和注意事项：
  - 对于理想运放，闭环电压增益是运放外电阻比值的函数，与运放内部的参数无关。
  - 增益中的负号表示 “反相” ，是反相放大电路名字的由来。
  - 反相放大电路中没有耦合电容（就是电容，作用是耦合所以叫耦合电容），因此反相放大电路可以放大直流电压信号。
反相放大电路扩展——带 T 型网络的放大电路
- 作为改进方案被提出的原因：
  
  反相放大电路的增益 $A_v$ 为 $-\frac{R_2}{R_1}$，那么如果我们的设计目标是设计一个闭环增益 $A_v=-100$ 且输入电阻 $R_i=R_1=50k\Omega$ 的反相放大电路。于是，反馈电阻 $R_2$ 就必须是 $5M\Omega$。然而，这个电阻值对大多数实际电路来说太大了。为了解决这个问题我们提出了作为改进方案的带 T 型网络的放大电路。
- 带 T 型网络的放大电路的电路图如图所示：
- 设 $R_2$、$R_3$ 和 $R_4$ 三个电阻的公共节点处电势为 $v_x$，则: \[ \begin{cases} \begin{aligned} &i_2+i_3=i_4\\\\ &\frac{v_1-v_x}{R_2}+\frac{v_x-v_o}{R_3}=\frac{v_x}{R_4}\\\\ &v_1=0 \end{aligned} \end{cases} \quad \Longrightarrow \quad A_v=\frac{v_o}{v_{i_1}}=-\frac{R_2}{R_1} \]
- 结论和注意事项：
  
  使用带 T 型网络的放大电路，可以在使用合理大小电阻的情况下获得更大的增益。
同相放大电路；
- 同相放大电路连接方式如图所示：
- 同相放大电路增益 $A_v=\frac{R_2}{R_1}+1$： \[ \begin{aligned} &\begin{cases} v_-=v_+=v_i\\\\ \frac{0-v_-}{R1}=\frac{v_--v_o}{R_2}\\ \end{cases}\\\\ &get\quad A_v=\frac{v_o}{v_i}=\frac{R_2}{R_1}+1 \end{aligned} \]
- 结论和注意事项：
电压跟随器：
- 电压跟随器连接方式如图所示：
- 电压跟随器增益 $A_v$：
- 结论和注意事项：
求和放大电路：
- 求和放大电路连接方式如图所示：
- 输出电压为 $v_o=-R_f\sum_{j=1}^{n}\frac{v_{i_j}}{R_i}$：
  
  \[ \sum_{j=1}^{n}\frac{v_{i_j}-0}{R_i}=\frac{0-v_o}{R_f}\\ get\quad v_o=-R_f\sum_{j=1}^{n}\frac{v_{i_j}}{R_i} \]
- 结论和注意事项：
差分放大电路：
- 差分放大电路连接方式如图所示：
- 输出电压为 $v_o=\frac{R_2}{R_1}(v_{i_2}-v_{i_1})$：
  
  $$
  \[\begin{aligned} &if\quad v_{i_2}=0,\;v_{i_1}\not=0\\ &then\quad v_{o_1}=-\frac{R_2}{R_1}v_{i_1}\\\\\\ &if\quad v_{i_2}\not=0,\;v_{i_1}=0\\ &then\quad v_{o_2}=\left(1+\frac{R_2}{R_1}\right)\left(1+\frac{R_4}{R_3+R_4}\right)v_{i_2}\\\\\\ &so\quad v_o=v_{o_1}+v_{o_2}=\left(1+\frac{R_2}{R_1}\right)\left(1+\frac{R_4}{R_3+R_4}\right)v_{i_2}-\frac{R_2}{R_1}v_{i_1}\\ &To\quad satified\quad when\quad v_{i_1}=v_{i_2},v_o=0\,;so\quad \frac{R_4}{R_3}=\frac{R_2}{R_1}\\ &Finally\quad v_o=\frac{R_2}{R_1}(v_{i_2}-v_{i_1}) \end{aligned}\]
  $$
- 结论和注意事项：
积分放大电路：
- 积分放大电路连接方式如图所示：
- 积分放大电路增益 $A_v$：
  
  \[ v_o=V_C-\frac{1}{RC}\int_{0}^{t}v_i(\tau)d\tau \]
- 结论和注意事项：
微分放大电路：
- 微分放大电路连接方式如图所示：
- 微分放大电路增益 $A_v$：
  
  \[ v_o=-RC\frac{dv_{i}}{dt} \]
- 结论和注意事项：
对数放大电路：
- 对数放大电路连接方式如图所示：
- 对数放大电路增益 $A_v$：
  
  \[ v_o=-V_Tln\left(\frac{v_i}{I_SR_1}\right) \]
- 结论和注意事项：
指数放大电路：
- 指数放大电路连接方式如图所示：
- 指数放大电路增益 $A_v$：
  
  \[ v_o=-I_SR\cdot e^{v_i/V_T} \]
- 结论和注意事项：
仪用放大电路：
- 仪用放大电路连接方式如图所示：
- 仪用放大电路增益 $A_v$：
  
  \[ v_o=\frac{R_4}{R_3}\left(1+\frac{2R_2}{R_1}\right)(v_{i_2}-v_{i_1}) \]
- 结论和注意事项：

集成电路偏置

使用分立电子元器件对晶体管放大电路进行偏置时，我们通常使用的是分压电阻网络。在集成电路设计中，电阻的集成需要比晶体管更大的面积，因此我们更希望通过晶体管来配置放大电路。在接下来的设计中我们可以看到，晶体管可以构成恒流源和负载器件。

集成电路偏置和有源负载这一章节学习了在设计集成电路中需要使用到的晶体管恒流源——镜像电流源（Current Mirror）和晶体管电阻（负载）——有源负载

关于集成电路的部分放到下一阶段学习吧

一个设计良好的电流源电路，必须同时满足如下这四点要求：

能够输出符合要求的直流电流；
温度稳定性更好；
受到电源电压等因素的影响较小；
输出电阻要尽可能更大；

如果一个电流源能够同时满足上述这些要求，那么就可以将其等效为下面的理想电流源：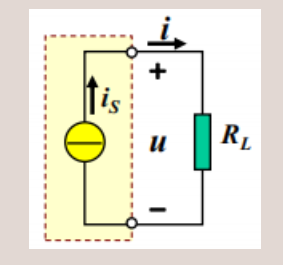

晶体管和场效应管等有源元件，在放大区的输出电流几乎不受输出电压的影响，展现出恒流特性：

差分和多级放大电路

本章介绍的是主要内容是一种多晶体管电路——差分放大电路。与之前理想运放一节不同的是，这里的差分放大电路是由基本的晶体管构成的电路

差分放大电路是模拟电路的基本单元，既是几乎所有运放的输入级，也是高速数字逻辑电路的基础。

差分放大电路为

施密特触发器

比较器

施密特触发器

放大电路

基本放大电路的构成

设计一个放大电路：

放大的概念：

放大电路的放大是指对于功率的放大，即小电流电压输入转化为一个大电流电压输出
本质：

功率放大的本质在于对能量的控制。

为了首先对能量的控制，我们必须在电路中引入一个控制能力的元件——有源元件，具体来说就是三极管和场效应管等。
前提：

合理放大信号的前提是不失真
测试：

在实验中我们使用正弦波进行信号放大的测试。

因为声波或其他各种波形，由傅里叶变换可以变换成多个正弦波的叠加，故只要电路系统可以正常的放大分解后的所有正弦波，就可以实现具体的设计目标。

因此在实验中我们使用正弦波进行放大的测试
放大电路的构建方法：
1. 目标：小功率转化为大功率
  - 小信号：小的什么程度：几毫伏或几十个毫伏
2. 条件：
  - 有源元件
  - 能量
3. 技术路线：
  - 三极管工作在放大状态下——即 $i_b$ 可以控制 $i_c$
  - 小信号控制 $i_b$
  - 合理的输出
\[ V_i（一个小信号输出电压）->放大电路->实现功率放大 \]

移相式振荡电路

移相式振荡电路，顾名思义，就是使相位发生移动来产生振荡的电路。

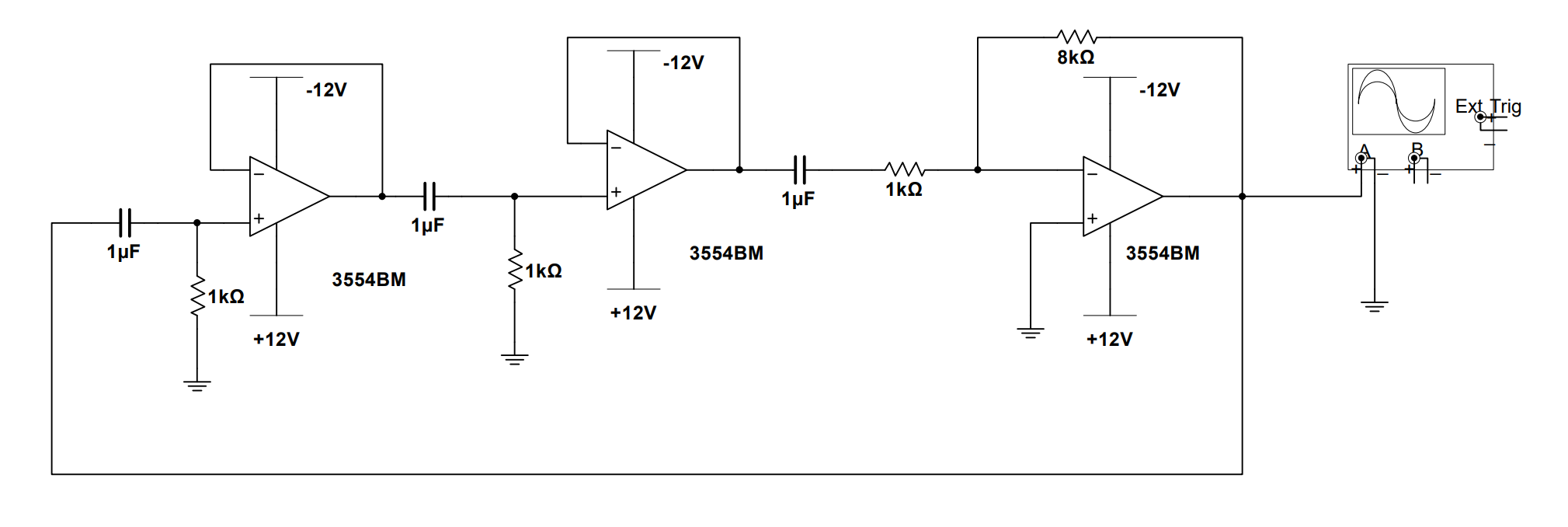
第一个要介绍的振荡电路是移相式振荡电路。移相式振荡电路如下图所示，由一个RC网络和一个反相放大器组成。可以看到放大器的输出即为振荡器的输出。接下来我们将进一步介绍这个振荡电路的细节。

实用移相式振荡电路示意图：

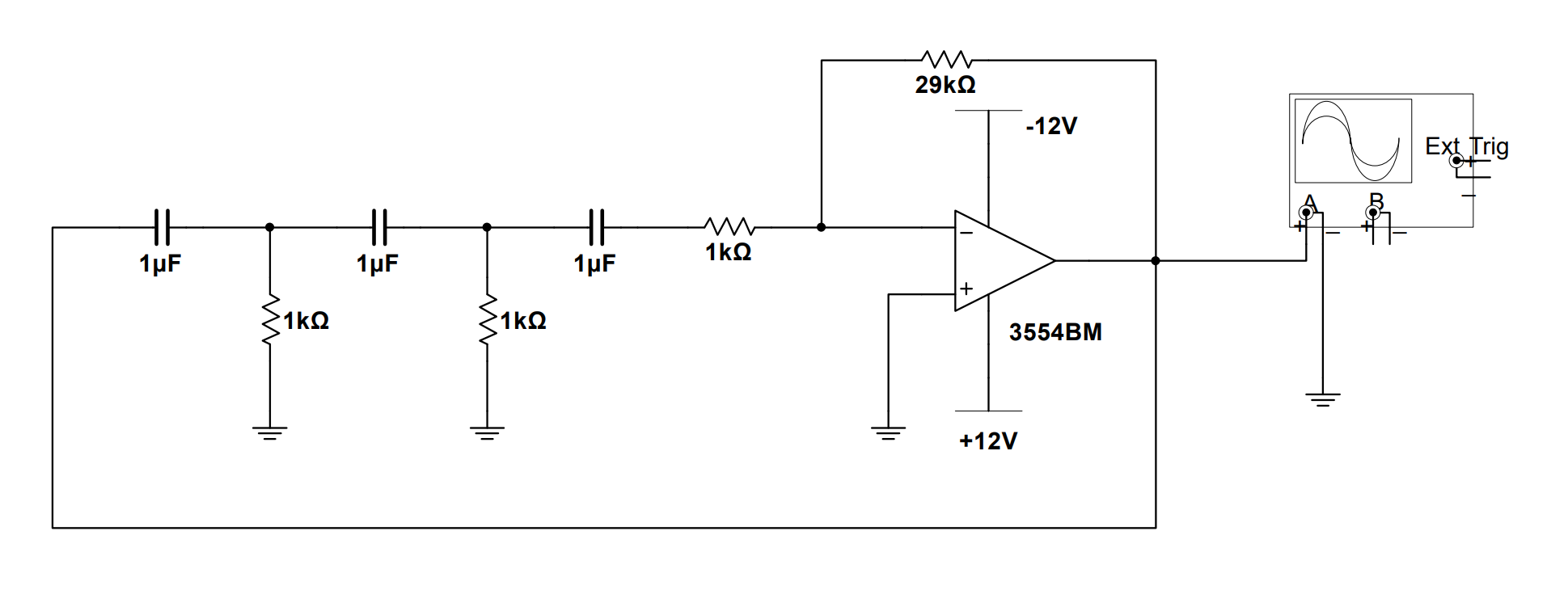
为了便于理解，我们将移相式振荡电路中的 RC 网络进行单独分析。在移相式振荡电路中，由于 $R_3$ 右边与运放的反相端相连，而运放的正相端与地相连，由于

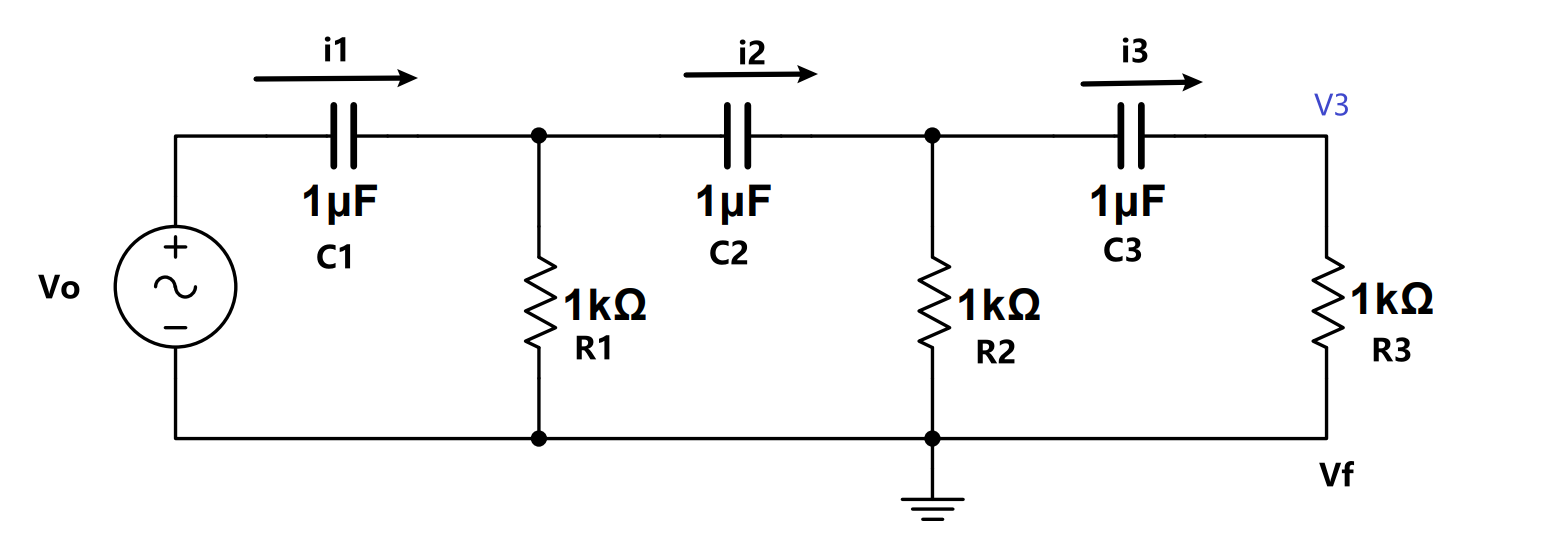\[ \begin{aligned} &-V_o + \frac{1}{sC}i_1 + R(i_1-i_2) = 0\\ &-R(i_1-i_2) + \frac{1}{sC}i_2 + R(i_2-i_3) = 0\\ &-R(i_2-i_3) + \frac{1}{sC}i_3 + Ri_3 = 0 \end{aligned} \] 由第三个式子得： \[ -R(i_2-i_3) + \frac{1}{sC}i_3 + Ri_3 = 0 \quad \longrightarrow \quad i_2 = \frac{\frac{1}{sC}+2R}{R}i_3 \] $i_2$ 带入第一个式子得： \[ -R(i_2-i_3) + \frac{1}{sC}i_3 + Ri_3 = 0 \quad \longrightarrow \quad i_1 = \frac{ (\frac{1}{sC}+2R)i_3 + V_o }{\frac{1}{sC}+R} \] $i_1,i_2$ 带入第二个式子得： \[ \begin{gather} -R(i_1-i_2) + \frac{1}{sC}i_2 + R(i_2-i_3) = 0\\ \downarrow \\ \left( \frac{\frac{1}{sC}+2R}{R} \right)i_2 = i_3 + i_1\\ \downarrow \\ \left( \frac{\frac{1}{sC}+2R}{R} \right)^2i_3 = i_3 +\frac{ \left( \frac{1}{sC}+2R \right)}{\frac{1}{sC}+R}i_3 + \frac{V_o}{\frac{1}{sC}+R}\\ \downarrow \\ \left(\frac{\frac{1}{(sC)^2}+\frac{4R}{sC}+4R^2}{R^2}-1-\frac{\frac{2}{sC}+3R}{\frac{1}{sC}+R}\right)i_3 = \frac{V_o}{\frac{1}{sC}+R}\\ \downarrow \\ i_3 = \frac{V_o}{\frac{1}{sC}+R} \cdot \left( \frac{R^2\left(\frac{1}{sC}+R\right)}{\frac{1}{(sC)^3}+\frac{5R}{(sC)^2}+\frac{6R^2}{sC}+R^3}\right)\\ \downarrow \\ i_3 = \left( \frac{R^2}{\frac{1}{(sC)^3}+\frac{5R}{(sC)^2}+\frac{6R^2}{sC}+R^3}\right)V_o \end{gather} \] 那么此时 $V_3$ 为 \[ V_3 = \left( \frac{R^2}{\frac{1}{(sC)^3}+\frac{5R}{(sC)^2}+\frac{6R^2}{sC}+R^3}\right)V_o \] 由图片可知对于上面的 RC 网络，传递函数 $H(s) = V_3/V_o$

故 RC 网络作为移相式振荡电路的选频网络时 \[ \beta(s) = H(s) = \frac{V_3}{V_o} = \left( \frac{R^3}{\frac{1}{(sC)^3}+\frac{5R}{(sC)^2}+\frac{6R^2}{sC}+R^3}\right) \] 为了满足 \[ T(s)=A(s)\beta(s)=1 \quad or \quad T(j\omega_0)=A(j\omega_0)\beta(j\omega_0)=-1 \] 且我们知道反相放大器的增益 $A(s)$ 为实数，故选频网络的 $\beta(s)$ 也应当是实数

我们将 $\beta(s)$ 展开为 $\beta(j\omega_0)$，以此观察如何确保 $\beta(s)$ 为实数：

首先我们有： \[ \begin{aligned} &\frac{1}{sC}=\frac{1}{j\omega C}=-\frac{j}{\omega C}\\ &\frac{1}{(sC)^2}=\frac{1}{(j\omega C)^2}=-\frac{1}{(\omega C)^2}\\ &\frac{1}{(sC)^3}=-\frac{1}{(\omega C)^2} \cdot -\frac{j}{\omega C} = \frac{j}{(\omega C)^3}\\ \end{aligned} \] 带入到 $\beta(s)$ \[ \beta(j\omega_0) = \left( \frac{R^3}{j\frac{1}{(\omega C)^3}-\frac{5R}{(\omega C)^2}-j\frac{6R^2}{\omega C}+R^3}\right) = \left( \frac{R^3}{j\left(\frac{1}{(\omega C)^3}-\frac{6R^2}{\omega C}\right)-\frac{5R}{(\omega C)^2}+R^3}\right) \] 则满足下式时 $\beta(s)$ 为实数 \[ \frac{1}{(\omega C)^3}-\frac{6R^2}{\omega C}=0 \] 解的 \[ \omega = \frac{1}{\sqrt{6}RC} \] 求解处的 $\omega$ 的含义是，当我们使用 RC 网络搭建电路时，若振荡器能正常振荡，则振荡频率可以使用这个公式进行计算。

那么如何配置电路从而让电路正常振荡呢？

电路正常振荡需要满足 $T(s)=A(s)\beta(s)=1$，缺一不可，因此选择完 RC 电路确定频率后，我们将 $\omega = \frac{1}{\sqrt{6}RC}$ 带入到 $\beta(j\omega_0)$ 中，得到 \[ \beta(j\omega_0) = \left( \frac{R^3}{-\frac{5R}{(\omega C)^2}+R^3}\right) = \frac{1}{1-\frac{5}{\omega^2C^2R^2}} = \frac{1}{1-\frac{5}{\frac{1}{6R^2C^2}R^2C^2}} = \frac{1}{1-30} = -\frac{1}{29} \] 那么可以求得 \[ A(j\omega_0) = \frac{T(j\omega_0)}{\beta(j\omega_0)}=\frac{-1}{-\frac{1}{29}}=29 \] 因此反相放大器的增益选择与 RC 网络无关，其值恒等于29.

移相式振荡电路总结： \[ \begin{gather}\omega = \frac{1}{\sqrt{6}RC}\\ A(j\omega_0) =29\end{gather} \]