信号与系统

发表于 2022-02-27 更新于 2022-07-31 Disqus：

信号

常见的奇异信号

奇异信号：函数中包含不连续点或其微分与积分有不连续点的函数，统称为奇异函数，也就是奇异信号。

名称	函数表达式
$f(t)$：单位斜变信号	$f(t) = \begin{cases} 0 & t<0 \\\\ t & t\ge0 \\ \end{cases}$
$ u(t)$：单位阶跃信号	$u(t) = \begin{cases} 0 & t<0 \\\\ 1 & t>0 \\ \end{cases}$
$\delta(t)$：单位冲激函数	$\begin{cases} \begin{aligned} &\int_{-\infty}^{\infty}\delta(t)dt = 1\\\\ &\delta(t) = 0\quad while(t\not=0) \end{aligned} \end{cases}$
$\delta(t)'$：冲激偶函数	$\delta(t)'=\frac{d\delta(t)}{dt}$

$f(t)$：单位斜变信号

单位斜变信号的“单位”体现在其非零部分的斜率为 $1$ 。

函数表达式： \[ f(t) = \begin{cases} 0 & t<0 \\\\ t & t\ge0 \\ \end{cases} \] 起始点移位 $t$ 后： \[ f(t-t_0) = \begin{cases} 0 & t<t_0 \\\\ t-t_0 & t\ge t_0 \\ \end{cases} \]

$ u(t)$：单位阶跃信号

函数表达式：

由表达式可知 $t=0$ 处函数未定义，可以将 $t=0$ 处函数值定义为 $u(0)=\frac{1}{2}$。 \[ u(t) = \begin{cases} 0 & t<0 \\\\ 1 & t>0 \\ \end{cases} \] 起始点移位 $t$ 后（或认为阶跃延时 $t$ 后），有： \[ u(t-t_0) = \begin{cases} 0 & t<t_0 \\\\ 1 & t>t_0 \\ \end{cases} \]

$\delta(t)$：单位冲激函数

狄拉克（Dirac）定义方式： \[ \begin{cases} \begin{aligned} &\int_{-\infty}^{\infty}\delta(t)dt = 1\\\\ &\delta(t) = 0\quad while(t\not=0) \end{aligned} \end{cases} \] 狄拉克（Dirac）定义表明：

除了坐标轴零点处，其余位置单位冲激函数的函数值均为 $0$ 。
单位冲激函数仅在一点处取值，而其面积（积分）为 $1$ ，由此可知单位冲激函数为长度为 $1$ 的线段：表示中我们使用长度为 $1$ 的向量来表示，方向与 $y$ 轴正半轴方向相同。

$\delta(t)'$：冲激偶函数

由符号可知冲激偶函数为冲激函数的导数。

常见奇异信号之间的关系：

\[ \begin{cases} \begin{aligned} &\frac{df(t)}{dt}=u(t)\\\\ &\frac{du(t)}{dt}=\delta(t)\\\\ &\delta(t)'=\frac{d\delta(t)}{dt} \end{aligned} \end{cases} \]

单位冲激函数 $\delta(t)$ 的简单性质：

单位冲激函数 $\delta(t)$ 具有抽样特性（也称“筛选”特性），$\delta(t)$ 可以用来筛选出信号中某一时刻的值（函数值），具体操作如下： \[ \int_{-\infty}^{\infty}\delta(t-t_0)f(t)dt=f(t_0) \] 解释：对于任意一个信号 $f(t)$ ，我们使用 $\delta(t)$ 可以筛选出目标的函数值 $f(t_0)$ 。
单位冲激函数 $\delta(t)$ 是一个偶函数，即 $\delta(t)=\delta(-t)$

线性时不变系统——LTI

理解线性：
1. 满足叠加性和均匀性
理解时不变特性：即系统本身的参数不随时间发生改变
线性时不变系统还具有的特性：
1. 微分特性：微分特性由线性和时不变性共同得出，内容为：
  
  若激励信号 $e(t)$ 可使系统产生响应信号 $r(t)$，则
  - 激励 $\frac{de(t)}{dt}$ 可产生响应 $\frac{dr(t)}{dt}$
  - 激励 $\frac{d^2e(t)}{dt}$ 可产生响应 $\frac{d^2r(t)}{dt}$，其余高阶求导同理
  - 激励 $\int^t_0e(\tau)d\tau$ 可产生响应 $\int^t_0r(\tau)d\tau$
2. 因果特性：因果特性描述了激励信号与响应信号之间的联系，因果特性表明：$t_0$ 时刻的响应只与$t=t_0$ 和 $t<t_0$ 时刻的输入有关，即激励和响应有着因果关系，只有有激励才会有响应。

分析LTI

系统建模就是使用数学工具例如方程或者微分方程来建立模型。

系统的数学描述方法可以分为两大类：

输入输出描述法——该方法注重系统激励和响应之间的关系，不关心系统内部变量情况
- 这种方法在数学上表现为一元$n$阶微分方程
状态变量描述法
- 可以给出系统响应
- 提供系统内部各变量的情况
- 可以用于多输入多输出系统的分析
- 这种方法在数学上表现为$n$元联立一阶微分方程

使用数学方法描述了一个系统后，我们就需要一些求解方法来求解系统模型，求解方法大体上也可以分为两类：

时域分析——时域分析是指在时间域上分析系统；前文可知系统可以简单理解为一个以时间为自变量的函数或函数族，时间域分析就是直接分析这个以时间变量作为自变量的函数。
- 时域分析分析输入输出法描述的系统模型时：
  - 可以使用经典的常系数微分方程和差分方程
  - 也可以使用算子符号来简化上面的微分方程和差分方程
  - 卷积是分析线性系统时域的重要数学工具
- 时域分析分析状态变量法描述的系统模型时：
  - 需要求解矩阵方程
变换域分析——变换域是指将时变函数中的自变量：时间变量变换成其他变量函数。变换域分析使得时域分析中复杂的微分积分运算变成了代数运算，将复杂的卷积运算变成了乘法运算

电系统的LTI数学模型建立

构成电系统的LTI模型表现为微分方程式

构成此类方程式的依据是电系统网络的两类约束特性：

电元器件约束特性——电子元器件的伏安特性
- 欧姆定律：
  - $V_R(t)=Ri_R(t)$
  - $V_L(t)=L\frac{di(t)}{dt}$
  - $V_C(t)=\frac{1}{C}\int_{-\infty}^ti_C{(\tau)}d\tau$
网络拓扑结构——网络结构决定的电流电压关系
- 基尔霍夫定律：
  - $\sum i(t)=0$
  - $\sum v(t)=0$

线性时不变系统的时域分析，微分方程的一般形式： \[ C_0\frac{d^nr(t)}{dt^n}+C_1\frac{d^{n-1}r(t)}{dt^{n-1}}+···+C_{n-1}\frac{dr(t)}{dt}+C_nr(t)=E_0\frac{d^me(t)}{dt^m}+E_1\frac{d^{m-1}e(t)}{dt^{m-1}}+···+E_{m-1}\frac{de(t)}{dt}+E_me(t) \] 上式可以缩写为： \[ \sum_{i=0}^nC_{n-i}\frac{d^ir(t)}{dt^i}=\sum_{j=0}^mE_{m-j}\frac{d^je(t)}{dt^j} \] 特殊形式，例如我们可以整理约束关系得到下式： \[ \frac{d^3r(t)}{dt^3}+7\frac{d^2r(t)}{dt^2}+16\frac{dr(t)}{dt}+12r(t)=e(t) \] 微分方程的全解由齐次解 $r_h(t)$ 和特解 $r_h(t)$ )组成，即： \[ r(t)=r_h(t)+r_h(t) \] 解法：

求齐次解 $r_h(t)$：

令 $\sum_{i=0}^nC_{n-i}\frac{d^ir(t)}{dt^i}=0$，该式称为齐次方程
将 $r(t)=Ae^{\alpha t}$ 代入齐次方程得 $\sum_{i=0}^nC_{n-i}\alpha^{i}=0$，称为特征方程
根据特征方程可以得齐次解 $r_h(t)$ 为
- 特征方程没有重根：
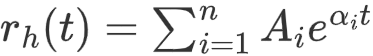
- 特征方程有重根：

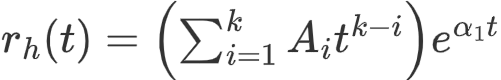
求特解 $r_h(t)$：

激励函数 $e(t)$	响应函数 $r(t)$ 的特解
$E$	$B$
$t^p$	$B_1t^p+B_2t^{p-1}+···+B_pt+B_{p+1}$
$e^{\alpha t}$	$Be^{\alpha t}$
$cos(\omega t)$	$B_1cos(\omega t)+B_2sin(\omega t)$
$sin(\omega t)$	$B_1cos(\omega t)+B_2sin(\omega t)$
$t^pe^{\alpha t}cos(\omega t)$	$(B_1t^p+···+B_pt+B_{p+1})e^{\alpha t}cos(\omega t)+(D_1t^p+···+D_pt+D_{p+1})e^{\alpha t}sin(\omega t)$
$t^pe^{\alpha t}sin(\omega t)$	$(B_1t^p+···+B_pt+B_{p+1})e^{\alpha t}cos(\omega t)+(D_1t^p+···+D_pt+D_{p+1})e^{\alpha t}sin(\omega t)$

求待定系数 $A$：

拉普拉斯变换

形态上，拉普拉斯变换做了这样一件事： \[ f(t)\xrightarrow{\sf{拉普拉斯变换}}F(s) \] 或者说： \[ f(t)\xrightarrow{\mathscr{L}\{f(t)\}}F(s) \] 从形态上讲，拉普拉斯变换将一个以时间 $t$ 为自变量的函数变换成了一个以频率 $s$ 为自变量的函数。

拉普拉斯变换将函数从时域变换到了频域，其实就是信号的自变量发生了变化。

意义：拉普拉斯变换可以将时域内的微分方程变换成频域内的代数方程，降低计算难度并且从频域再次回到时域时保证解不变。

$\mathscr{L}\{f(t)\}$ 拉氏变换的定义为： \[ \mathscr{L}\{f(t)\}=\int_{0}^{\infty}f(t)\cdot e^{-st}dt \] 注意事项：

进行拉氏变换的 $f(t)$ 是否存在的问题：
- 首先是初等函数都能进行拉氏变换
- 默认在线性电路分析中均使用能够进行拉氏变换的电源进行系统的激励
上述拉氏变换也可以称作单边拉氏变换，此变换忽略了 $t<0$ 时的 $f(t)$
$t<0$ 时的 $f(t)$ 可以通过初始条件来考虑

分类：

学习拉普拉斯变换将拉普拉斯变换分为函数变换和算子变换

函数变换：研究初等函数的拉氏变换
算子变换：研究一般函数的拉氏变换

算子变换：

拉氏变换	$\mathscr{L}\{f(t)\}=F(s)$
乘以常数	$\mathscr{L}\{Kf(t)\}=KF(s)$
加减运算	$\mathscr{L}\{f(t_1)+f(t_2)-f(t_3)\}=F(s_1)+F(s_2)-F(s_3)$
微分运算	一重微分：$\mathscr{L}\{\frac{df(t)}{dt}\}=sF(s)-f(0^-)$ $n$ 重微分：$\mathscr{L}\{\frac{d^nf(t)}{dt^n}\}=s^nF(s)-s^{n-1}f(0^-)-\sum_{i=2}^{n}s^{n-i}\frac{d^{i-1}f(0^-)}{dt^{i-1}}$
积分运算	$\mathscr{L}\{\int_{0^-}^{t}f(t)dt\}=F(s)/s$
时域平移特性	$\mathscr{L}\{f(t-a)\cdot u(t-a)\}=e^{-as}\cdot F(s),\quad a>0$ $\mathscr{L}\{e^{-as}\cdot F(s)\}=F(s+a)$
尺度变换特性	$\mathscr{L}\{f(at)\}=\frac{1}{a}F\left(\frac{s}{a}\right),\quad a>0$

傅里叶分析简介

傅里叶定理表明，任何一个角频率为$\omega_0$的周期函数都可以表示为无穷多个频率为$\omega_0$整数倍的正弦函数与余弦函数之和。

对于一个周期函数$f(t)$，若满足Dirichlet条件，则该周期函数可以展开成傅里叶级数，即： \[ \begin{aligned} &if\quad f(t)=f(t+T)\\\\ &then\quad f(t)=a_0 + \displaystyle\sum_{n=1}^{\infty}a_ncos(n\omega_0t) + \displaystyle\sum_{n=1}^{\infty}b_nsin(n\omega_0t)\\ &\boxed { \begin{aligned} &a_0=\frac{1}{T}\int^{T}_{0}f(t)\,dt\\ &a_n=\frac{2}{T}\int^{T}_{0} f(t) cos(n\omega_0t) \,dt \\ &b_n=\frac{2}{T}\int^{T}_{0} f(t) cos(n\omega_0t) \,dt \\ \end{aligned} } \end{aligned} \]

\[ \begin{aligned} &if \quad f(t)=f(-t)\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\;\,\\\\ &\boxed { \begin{aligned} &a_0=\frac{2}{T}\int^{T/2}_{0}f(t)\,dt\\ &a_n=\frac{4}{T}\int^{T/2}_{0} f(t) cos(n\omega_0t) \,dt \\ &b_n=0 \\ \end{aligned} } \end{aligned} \]

展开式中$a_0$称为直流分量，其值等于函数$f(t)$的平均值；$a_n$与$b_n(n\not=0)$是交流分量的幅值 \[ f(t)=f(t+T)\Rightarrow f(t)=a_0 + \displaystyle\sum_{n=1}^{\infty}a_ncos(n\omega_0t) + \displaystyle\sum_{n=1}^{\infty}b_nsin(n\omega_0t)\\ \]

\[ \begin{array}{c|c|c} \begin{aligned} &general\quad condition\\ &\boxed { \begin{aligned} &a_0=\frac{1}{T}\int^{T}_{0}f(t)\,dt\\ &a_n=\frac{2}{T}\int^{T}_{0} f(t) cos(n\omega_0t) \,dt \\ &b_n=\frac{2}{T}\int^{T}_{0} f(t) sin(n\omega_0t) \,dt \\ \end{aligned} } \end{aligned} & \begin{aligned} &if \quad f(t)=f(-t)\\ &\boxed { \begin{aligned} &a_0=\frac{2}{T}\int^{T/2}_{0}f(t)\,dt\\ &a_n=\frac{4}{T}\int^{T/2}_{0} f(t) cos(n\omega_0t) \,dt \\ &b_n=0 \\ \end{aligned} } \end{aligned} & \begin{aligned} &if \quad f(t)=-f(-t)\\ &\boxed { \begin{aligned} &a_0=0\\ &a_n=0\\ &b_n=\frac{4}{T}\int^{T/2}_{0} f(t) sin(n\omega_0t) \,dt \\ \end{aligned} } \end{aligned}\\ \end{array}\\ \]

\[ P_{1\Omega}=F_{rms}^2=a_0^2+\frac{1}{2}\displaystyle\sum_{n=1}^{\infty}(a_n^2+b_n^2) \]

线性系统：

线性系统是指具有叠加性和均匀性的系统：

叠加性：多个激励同时作用时产生的响应 = 多个激励分别作用时产生的响应的和
均匀性：输入增益于输出增益相同

\[ v_R(t)=Ri_R(t)\\ v_L(t)=L\frac{i_L(t)}{dt}\\ v_C(t)=\frac{1}{C}\int_{-\infty}^{t}i_C(\tau)d\tau \]

\[ V_L(t)+V_R(t)+V_C(t)=e(t)\\ L\frac{i_L(t)}{dt}+Ri_R(t)+\frac{1}{C}\int_{-\infty}^{t}i_C(\tau)d\tau=e(t)\\ L\frac{d^2i_L(t)}{dt^2}+R\frac{di_R(t)}{dt}+\frac{1}{C}i_C(t)=\frac{de(t)}{dt}\\ 对于串联，有i_L=i_R=i_C\\ L\frac{d^2i(t)}{dt^2}+R\frac{di(t)}{dt}+\frac{1}{C}i(t)=\frac{de(t)}{dt}\\ \]

\[ i_R(t)=\frac{1}{R}v(t)\\ i_L(t)=\frac{1}{L}\int_{-\infty}^{t}v(\tau)d\tau\\ i_C(t)=C\frac{dv_C(t)}{dt} \]

\[ i_C(t)+i_R(t)+i_L(t)=i_S(t)\\ C\frac{d^2v(t)}{dt^2}+\frac{1}{R}\frac{dv(t)}{dt}+\frac{1}{L}v(t)=\frac{di_S(t)}{dt}\\ \]

若组成系统的都是参数恒定的线性元件，则相应的数学模型是一个线性常系数常微分方程，若各器件初始无储能，则为一个线性时不变系统

则对于一个线性时不变系统来说，其数学模型可以使用一个微分方程来描述： \[ C_0\frac{d^nr(t)}{dt^n}+C_1\frac{d^{n-1}r(t)}{dt^{n-1}}+···+C_{n-1}\frac{dr(t)}{dt}+C_nr(t)=E_0\frac{d^me(t)}{dt^m}+E_1\frac{d^{m-1}e(t)}{dt^{m-1}}+···+E_{m-1}\frac{de(t)}{dt}+E_me(t) \] 方程的解可以记作： $$

线性电路系统由线性电子元器件构成，描述此类系统需要借助电路网络的两类约束条件：

元件约束特性
网络拓扑约束

两种约束的数学描述可以由微分方程组给出，这类方程组称为系统的状态方程

我们联立上述方程组可以得到一个高阶微分方程，这个高阶微分方程称作输入输出方程，其阶数为系统的阶数

系统的输入称为激励，输出称为响应；若能给出系统的初始状态和激励，则可以获得响应

系统的初始状态由若干独立条件给出，独立条件的个数与系统的阶数相同

线性时不变系统一般使用一个n阶线性微分方程来描述

这个方程可以被整理为： \[ \sum_{i=0}^nC_{n-i}\frac{d^ir(t)}{dt^i}=\sum_{j=0}^mE_{m-j}\frac{d^je(t)}{dt^j} \] 一般来说，对于响应，其有实际意义的定义域称为响应区间，即：$0_+ \le t< \infty$

$e(t)$加入前，系统为起始状态（$0_-$状态） \[ r^k(0_-)=[r(0_-),\frac{d}{dt}r(0_-),...,\frac{d^n}{dt^n}r(0_-)] \]

$e(t)$加入后，系统为初始状态（$0_+$状态） \[ r^k(0_+)=[r(0_+),\frac{d}{dt}r(0_+),...,\frac{d^n}{dt^n}r(0_+)] \] 因此，决定关系为：

起始状态 $+$ $e(t)$ $\rightarrow$ 初始状态
初始状态 $\rightarrow$ 响应齐次解的常系数 $A$

响应可以拆解为三种形式：

固有响应 $+$ 受迫响应
零输入响应 $+$ 零状态响应
暂态响应 $+$ 稳态响应

全响应：

对于使用$n$阶微分方程描述的线性系统： \[ \sum_{i=0}^nC_{n-i}\frac{d^ir(t)}{dt^i}=\sum_{j=0}^mE_{m-j}\frac{d^je(t)}{dt^j} \] 上述微分方程的解，即系统的响应，为：$r(t)=r_h+r_p$，求解步骤为：

使用特征根求解待定系数的齐次解
使用待定系数法求解特解
求解齐次解中的系数
- 使用 $r^k(0_+)=[r(0_+),\frac{d}{dt}r(0_+),...,\frac{d^n}{dt^n}r(0_+)]$ 来求解系数向量 $A_n$
- 寻找 $r^k(0_-)$ 与 $r^k(0_+)$ 之间的关系
  - 物理法：对于电路系统来说即换路定理：电容电感端性质的连续性
  - 数学法：冲激函数匹配法：微分方程两端保持各阶奇异函数的平衡

固有响应和受迫响应：

$r(t)=r_h+r_p$ \[ r(t)=\underbrace_{\sf{固有响应}}+\underbrace_{\sf{受迫响应}} \]

零输入响应和零状态响应：

零输入响应： \[ \sum_{i=0}^nC_{n-i}\frac{d^ir(t)}{dt^i}=0 \] 其中 \[ \sum_{j=0}^mE_{m-j}\frac{d^je(t)}{dt^j}=0 \] 说明 \[ [r(0_+),\frac{d}{dt}r(0_+),...,\frac{d^n}{dt^n}r(0_+)]=r^k(0_-)=[r(0_-),\frac{d}{dt}r(0_-),...,\frac{d^n}{dt^n}r(0_-)] \] 零状态响应： \[ \sum_{i=0}^nC_{n-i}\frac{d^ir(t)}{dt^i}=\sum_{j=0}^mE_{m-j}\frac{d^je(t)}{dt^j} \] 但是与全响应不同的是，零状态响应中： \[ r^k(0_-)=[r(0_-),\frac{d}{dt}r(0_-),...,\frac{d^n}{dt^n}r(0_-)]=[0,0,...,0] \] 其余求法依旧是：

使用特征根求解待定系数的齐次解
使用待定系数法求解特解
求解齐次解中的系数

注意：先求特解再求系数不要乱！

使用特征根求解待定系数的齐次解
使用待定系数法求解特解
求解齐次解中的系数：使用 $r^k(0_+)=[r(0_+),\frac{d}{dt}r(0_+),...,\frac{d^n}{dt^n}r(0_+)]$ 来求解系数向量 $A_n$

如何从微分方程上判断线性系统

只能出现函数本身，以及函数的任何阶次的导函数；
函数本身跟所有的导函数之间除了加减之外，不可以有任何运算；
函数本身跟本身、各阶导函数本身跟本身，都不可以有任何加减之外的运算；
若有积分项，被积函数应为输入变量，如 $\int_{-\infty}^{t}r(\tau)d\tau$。其实积分就是微分的负次幂。
不允许对函数本身、各阶导函数做任何形式的复合运算。

线性微分方程与非线性微分方程的区别是什么？

名称	函数表达式
\(f(t)\)：单位斜变信号	\(f(t) = \begin{cases} 0 & t<0 \\\\ t & t\ge0 \\ \end{cases}\)
$ u(t)$：单位阶跃信号	\(u(t) = \begin{cases} 0 & t<0 \\\\ 1 & t>0 \\ \end{cases}\)
\(\delta(t)\)：单位冲激函数	\(\begin{cases} \begin{aligned} &\int_{-\infty}^{\infty}\delta(t)dt = 1\\\\ &\delta(t) = 0\quad while(t\not=0) \end{aligned} \end{cases}\)
\(\delta(t)'\)：冲激偶函数	\(\delta(t)'=\frac{d\delta(t)}{dt}\)

激励函数 \(e(t)\)	响应函数 \(r(t)\) 的特解
\(E\)	\(B\)
\(t^p\)	\(B_1t^p+B_2t^{p-1}+···+B_pt+B_{p+1}\)
\(e^{\alpha t}\)	\(Be^{\alpha t}\)
\(cos(\omega t)\)	\(B_1cos(\omega t)+B_2sin(\omega t)\)
\(sin(\omega t)\)	\(B_1cos(\omega t)+B_2sin(\omega t)\)
\(t^pe^{\alpha t}cos(\omega t)\)	\((B_1t^p+···+B_pt+B_{p+1})e^{\alpha t}cos(\omega t)+(D_1t^p+···+D_pt+D_{p+1})e^{\alpha t}sin(\omega t)\)
\(t^pe^{\alpha t}sin(\omega t)\)	\((B_1t^p+···+B_pt+B_{p+1})e^{\alpha t}cos(\omega t)+(D_1t^p+···+D_pt+D_{p+1})e^{\alpha t}sin(\omega t)\)

拉氏变换	\(\mathscr{L}\{f(t)\}=F(s)\)
乘以常数	\(\mathscr{L}\{Kf(t)\}=KF(s)\)
加减运算	\(\mathscr{L}\{f(t_1)+f(t_2)-f(t_3)\}=F(s_1)+F(s_2)-F(s_3)\)
微分运算	一重微分：\(\mathscr{L}\{\frac{df(t)}{dt}\}=sF(s)-f(0^-)\) \(n\) 重微分：\(\mathscr{L}\{\frac{d^nf(t)}{dt^n}\}=s^nF(s)-s^{n-1}f(0^-)-\sum_{i=2}^{n}s^{n-i}\frac{d^{i-1}f(0^-)}{dt^{i-1}}\)
积分运算	\(\mathscr{L}\{\int_{0^-}^{t}f(t)dt\}=F(s)/s\)
时域平移特性	\(\mathscr{L}\{f(t-a)\cdot u(t-a)\}=e^{-as}\cdot F(s),\quad a>0\) \(\mathscr{L}\{e^{-as}\cdot F(s)\}=F(s+a)\)
尺度变换特性	\(\mathscr{L}\{f(at)\}=\frac{1}{a}F\left(\frac{s}{a}\right),\quad a>0\)

信号